Macaulay Duration: Overview, How it Works, Formula, and Calculation

What is Macaulay Duration?

Macaulay Duration is the weighted average time it takes for an investor to receive the bond's cash flows (coupon payments and principal repayment). It is expressed in years and helps measure a bond's sensitivity to interest rate changes.

Developed by economist Frederick Macaulay in 1938, this concept is widely used in fixed-income markets to assess a bond's price volatility and investment risk.

The longer the Macaulay duration, the higher the bond’s interest rate risk.

Shorter durations indicate an investor will recover its investment faster, reducing exposure to rate fluctuations.

How Does Macaulay Duration Work?

A bond investor has mainly 3 types of risk to consider:

• Price Risk: Risk of change in bond’s price due to changing interest rates.
• Re-investment Risk: Risk of re-investing a bond's interest income at much lower interest rates.
• Credit Risk: When the bond issuer is at risk of paying back interest and principal.

Macaulay’s Duration mainly addresses price and re-investment risk. When you calculate duration, it tells you the appropriate time horizon that balances both of these risks.

You will understand this concept further when we look at the calculation of Macaulay’s Duration.

Macaulay Duration Formula

The formula for duration is a technical one, and is as follows;

Where:

How to calculate Macaulay Duration

We can understand the calculation with the help of a small example. Consider a bond with the following features:

• Face Value = $1,000
• Coupon Rate = 5% (paid annually)
• Maturity = 3 years
• Yield to Maturity (YTM) = 4%
• Price of the bond = $1027.79

Step 1: Calculate the Present Value of Each Cash Flow

Step 2: Multiply Each PV by Its Corresponding Year

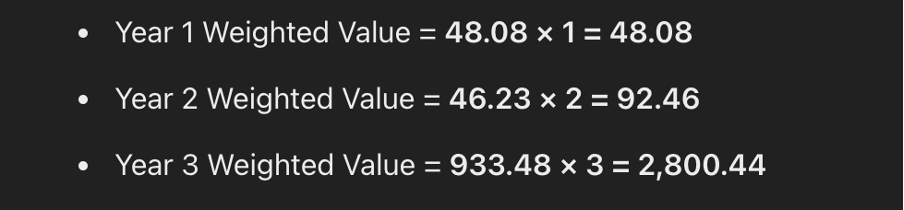
Step 3: Sum up the Weighted Values

Step 4: Divide by the Bond Price

A duration of 2.86 years means that the investor will, on average, take 2.86 years for the investor to recover its investment through the bond’s periodic cash flows (coupon payments) and the final principal repayment.

It also represents the point at which price risk and reinvestment risk offset each other.

• If an investor’s investment horizon matches the bond’s Macaulay Duration, the combined impact of price risk and reinvestment risk is minimized.
• In this scenario, any loss from a bond’s price decline (if rates rise) is balanced by the higher reinvestment rates available for future cash flows — and vice versa.

Suppose an investor has a 3-year investment horizon.

• If they invest in a bond with a Macaulay Duration of 2.86 years, their investment is well-aligned.
• Even if interest rates fluctuate during this period, the combination of cash flow reinvestment and bond price movement will help offset each other, reducing overall risk.

Factors Affecting Macaulay Duration

Several factors influence a bond’s duration:

• Time to Maturity:

• Longer maturity = Higher duration (more exposure to interest rate changes).
• Shorter maturity = Lower duration (less risk).

• Coupon Rate:

• Higher coupon rates = Lower duration because more cash flow is received earlier.
• Lower coupon rates = Higher duration as most cash flow is delayed until maturity.

• Yield to Maturity (YTM):

• As YTM increases, duration decreases because future cash flows are discounted more heavily.

Macaulay Duration vs. Modified Duration

While both metrics measure interest rate risk, they differ in their purpose and calculation:

Aspect	Macaulay Duration	Modified Duration
Meaning	Measures the weighted average time to recover investment.	Measures a bond's price sensitivity to interest rate changes.
Unit of Measure	Expressed in years.	Expressed as a percentage change in price per 1% interest rate change.
Calculation	Focuses on the timing of cash flows.	Derived from Macaulay Duration using this formula:

Conclusion

Calculating Macaulay’s duration is lengthy and is only useful if you want to compare 2 bonds with fixed cashflows and figure out the weighted average time till you receive your investment.

Figuring out the weighted average time can lead you to balance price and reinvestment risk.

Whether you are a CFA candidate or working in the fixed-income sector, understanding Macaulay Duration is crucial for understanding bonds and managing portfolios.